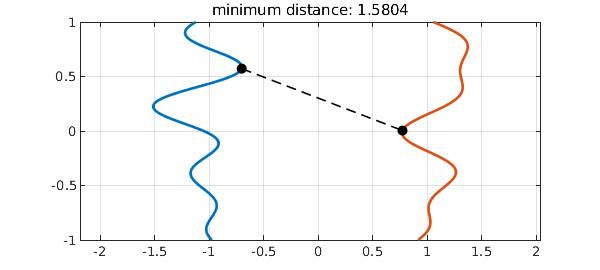
Suppose we have two curves, like these,

tic, rng(1), LW = 'linewidth'; MS = 'markersize';
t = chebfun('t');
f = 1i*t + .2*randnfun(.5) - 1;
g = 1i*t + .2*randnfun(.5) + 1;
plot([f g],'linewidth',2), axis equal, grid on

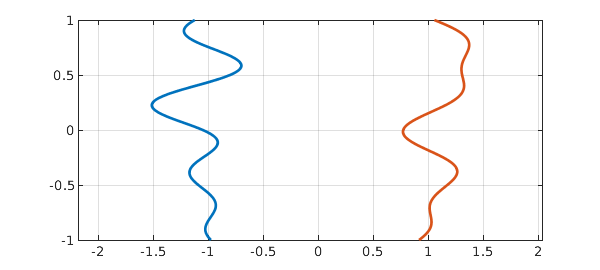
and we want to know the closest distance between them. (This is a great simplification of a problem John Maddocks brought up at lunch today.) I am sure there is a lot known about how to compute this.

One approach is to simply make a chebfun2 $d(x,y)$ representing the distance between $f(x)$ and $g(y)\dots$

d = chebfun2(@(x,y) abs(f(x)-g(y)));
contour(d,LW,1), axis equal, colorbar, xlabel x, ylabel y

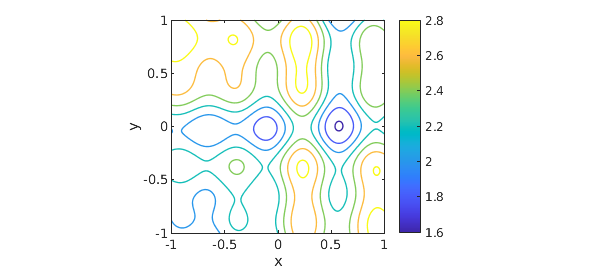
$\dots$ and find the global minimum:

[mindist,pos] = min2(d); x = f(pos(1)); y = g(pos(2));
plot([f g],'linewidth',2), axis equal, grid on
hold on, plot([x y],'--k',LW,1.2), plot([x y],'.k',MS,20), hold off
title(['minimum distance: ' num2str(mindist)]), toc

Elapsed time is 2.990995 seconds.