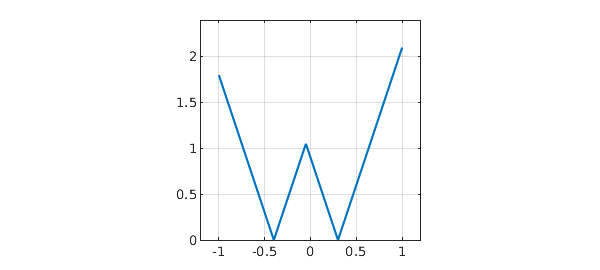
Here is a function with the shape of a W:
t = chebfun(@(t) t); f = 3*min(abs(t+.4),abs(t-.3)); ax = [-1.2 1.2 0 2.4]; plot(f), axis(ax), axis square, grid on
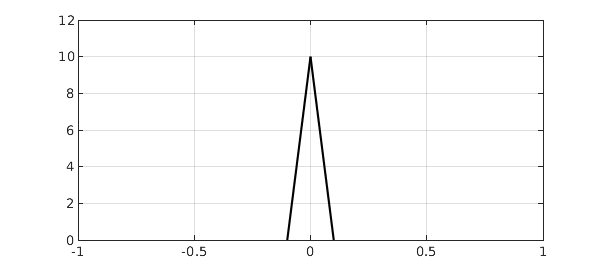
And here is a narrow function with integral equal to $1$:
h = 0.1; s = chebfun(@(s) s,[-h h]); g = (h-abs(s))/h^2; plot(g,'k'), axis([-1 1 0 12]), grid on
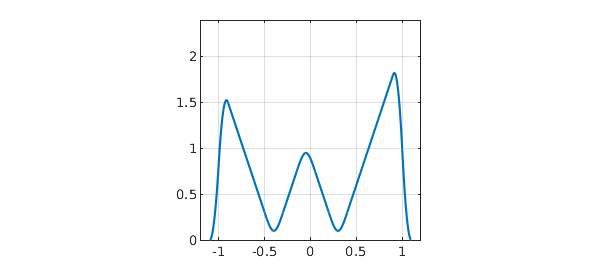
If we convolve the two functions, we get a W with rounded corners. At the ends, the "rounding" has brought the values down to $0$:
f2 = conv(f,g); plot(f2), axis(ax), axis square, grid on
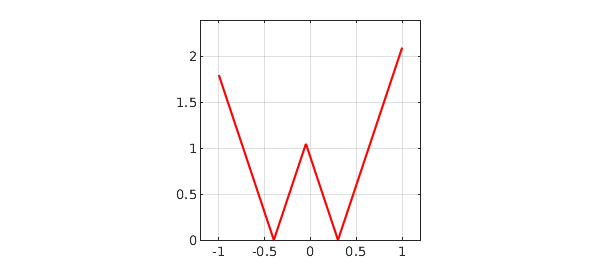
Let's try a similar but different computation in which the W is not a real function of a real variable, but a complex function of a real parameter. Here is that complex function:
W = t + 1i*f(t); plot(W,'r'), axis(ax), axis square, grid on
And here is its convolution with g:
W2 = conv(W,g); plot(W2,'r'), axis(ax), axis square, grid on
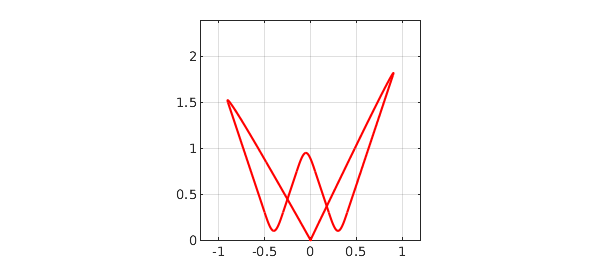
Do you understand why this picture looks different from the previous one?

