Order stars are a beautiful idea of complex analysis that resolved several open conjectures when they were introduced in 1978 by Wanner, Hairer, and Norsett [1,2,3]. Chebfun is not really a very good tool for illustrating them, since there are poles involved that must be smashed away, but let us give it a go.
Let $R(z)$ be a function of the complex variable $z$. The order star of $R$ is the region bounded by the curve(s) in the plane satisfying the condition
$$ | e^{-z} R(z)| = 1 . $$
For example, here is a function handle for the type $(2,3)$ Pade approximant of $e^z$:
c = 1./factorial(0:18); r = padeapprox(c,2,3);
We can use this mollifying function to turn poles into constants while preserving the absolute value $f=1$:
smash = @(f) tanh(abs(f).^2)/tanh(1);
Now we can plot the order star like this:
d = 6*[-1 1 -1 1]; f = chebfun2(@(z) smash(r(z).*exp(-z)),d); star = roots(f-1); plot(star,'k','linewidth',1.6) axis(d), axis square
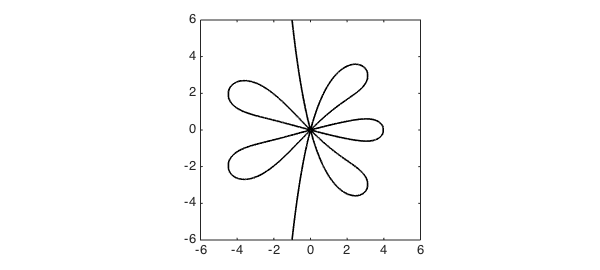
Such figures reveal important properties of the function $R$. For example, the meeting of 12 sectors at the origin reflects the 6th-order agreement of the Pade approximant with $e^z$,
$$ e^z - R(z) = O(z^6). $$
References
-
E. Hairer and G. Wanner, Solving Ordinary Differential Equations II, 2nd revised ed., Springer, 1996.
-
A. Iserles and S. P. Norsett, Order Stars, Chapman and Hall, 1991.
-
G. Wanner, E. Hairer, and S. P. Norsett, Order stars and stability theorems, BIT, 18 (1978), 475-489.

