The Frank-Kamenetskii or "spontaneous combustion" equation is the PDE
$$ {\partial u\over \partial t} = {\partial^2u\over \partial x^2} + A\exp(u). $$
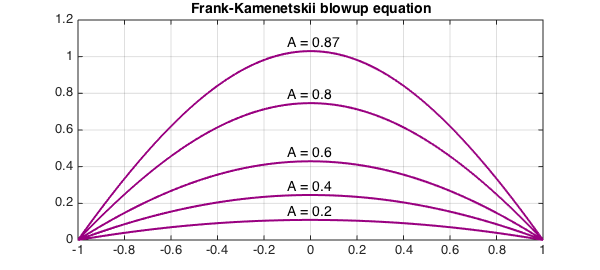
On the interval $[-1,1]$ with zero initial and boundary conditions, solutions to this equation blow up to infinity in finite time if $A$ is bigger than about $0.878$. For smaller $A$, solutions converge to a steady state.
Here we compute some of these steady-state solutions, which are solutions of the ODE boundary value problem
$$ u''+A\exp(u)=0,\qquad u(-1)=u(1)=0. $$
N = chebop([-1 1]);
N.bc = 'dirichlet';
FS = 'fontsize';
for A = [.2 .4 .6 .8 .87]
N.op = @(u) diff(u,2) + A*exp(u);
u = N\0;
plot(u,'color',[.6 0 .5],'linewidth',2), grid on, hold on
text(-.1,max(u)+.04,['A = ' num2str(A)],FS,14)
end
axis([-1 1 0 1.2])
title('Frank-Kamenetskii blowup equation',FS,14)
References
- H. Fujita, On the nonlinear equations $\Delta u + \exp(u) = 0$ and $dv/dt = \Delta v + \exp(v)$, Bulletin of the American Mathematical Society, 75 (1969), 132-135.