This example shows how easy it is to solve one of the example problems from the Oxford MSc in Mathematical Modelling and Scientific Computing week 0 MATLAB 'Crash Course' using Chebfun. (And also how easy it is to make a Chebfun Example!).

Problem. For what values of $a$ does

$$ I(a) = \int_{-1}^1 \sin(x) + \sin(a x^2) dx = 1 ? $$

Solution. Define the integrand as a function of $x$ and $a$.

F = @(x,a) sin(x) + sin(a*x.^2);

For a given $a$, we can compute the integral using Chebfun's sum command.

I = @(a) sum(chebfun(@(x) F(x,a)));

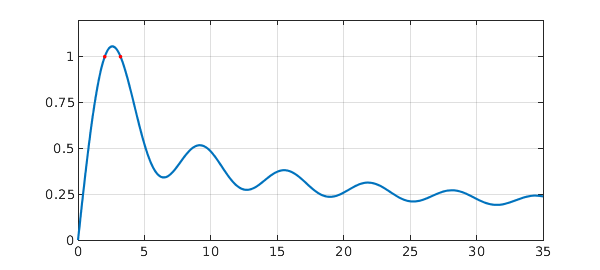
We compute a chebfun of this result, for $a$ ranging from $0$ to $100$.

Ia = chebfun(@(a) I(a),[0 100]);

We use Chebfun's roots command to find where $I(a)=1$.

r = roots(Ia-1)

r =
   2.011698636650816
   3.199526913460049

We plot this, to make sure it looks sensible.

plot(Ia), hold on, grid on
axis([0 35 0 1.2]), set(gca,'ytick',0:.25:1)
plot(r,Ia(r),'.r');

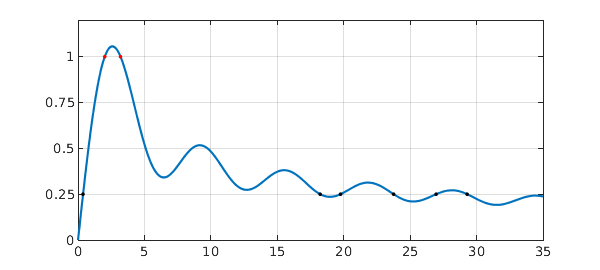
Since we have $I(a)$ as a chebfun, we can do other things, like find where $I(a) = 0.25$

r = roots(Ia-0.25)
plot(r,Ia(r),'.k'), hold off

r =
   0.378866771015907
  18.225950880000607
  19.761174831761743
  23.753831561562023
  26.956276286229951
  29.291546747613683

or the value of $a$ which maximises $I(a)$

m = max(Ia)

m =
   1.056688680049085

or the standard deviation of the gaps between the local minima for $a\in [0,100]$.

[y x] = min(Ia,'local');
f = std(diff(x(2:end-1)))

f =
   0.008984009280341