[revised June 2019]

Here is the Bessel function $J_0$ on the interval $[0,100]$.

J0 = chebfun(@(x) besselj(0,x),[0 100]);
figure, plot(J0), grid on
title('Bessel function J_0')

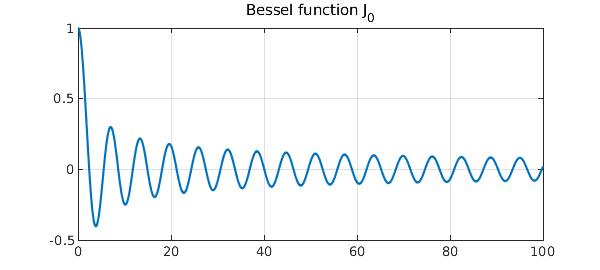
We can find its roots like this:

r = roots(J0);
hold on, plot(r,J0(r),'.r')

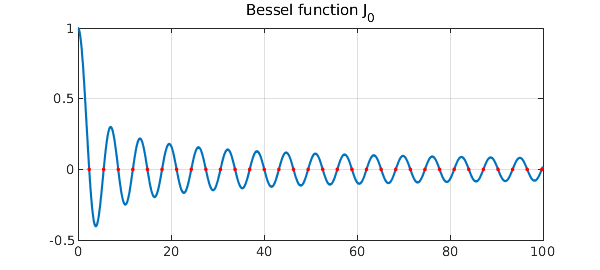
The number of roots can be found with the length command:

number_of_roots = length(r)

number_of_roots =
    32

Suppose you wanted to know the numbers of roots in various intervals $[a,b]$. You could define an anonymous function:

rootsab = @(a,b) length(roots(chebfun(@(x) besselj(0,x),[a b])));

For example:

tic
disp('Number of roots between 1000000 and 1001000:')
n = rootsab(1000000,1001000)
toc

Number of roots between 1000000 and 1001000:
n =
   318
Elapsed time is 0.077299 seconds.