Assume that $f(x,y,z)$ is a function defined over the unit 2-sphere in three dimensions. Our aim is to explore the building blocks of $f$ using the partition command. Let's start with a spherefun object:

f = spherefun(@(x,y,z) 0.5 + sinh(5*x.*y.*z).*cos(x-y+2*z))
plot(f), axis off, hold on
contour(f, 'color','k'),

f =
   spherefun object
       domain        rank    vertical scale
     unit sphere      21          1.6

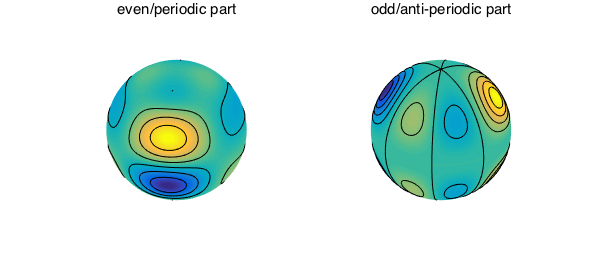
A spherefun can be seen as a sum of two spherefuns, one of them even/$\pi$-periodic and the other odd/$\pi$-anti-periodic [1]. Recall that a univariate function $g$ is $\pi$-anti-periodic if $g(x+\pi) = -g(x)$. The command `[fep, foa] = partition(f)' partitions $f$ accordingly.

[fep, foa] = partition(f)
err = norm(fep+foa - f)

subplot(1,2,1), plot(fep), hold on, contour(fep,'k')
title('even/periodic part'), axis off
subplot(1,2,2), plot(foa), hold on, contour(foa,'k')
title('odd/anti-periodic part'), axis off, axis off, hold off

fep =
   spherefun object
       domain        rank    vertical scale
     unit sphere      11          1.2
foa =
   spherefun object
       domain        rank    vertical scale
     unit sphere      10          0.94
err =
     0

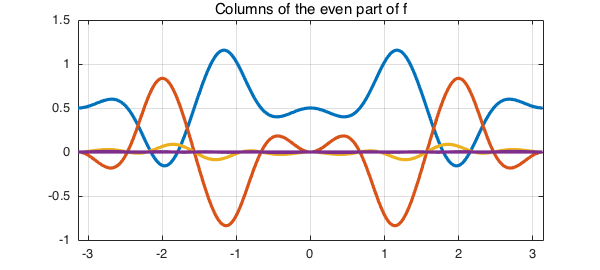
fep has a CDR decomposition [1] whose columns are even and whose rows are $\pi$-periodic (not just $2\pi$!):

[Ce, D, Rp] = cdr(fep);
clf, plot(Ce)
grid on, title('Columns of the even part of f')

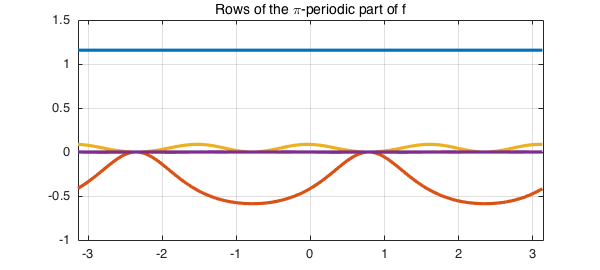
clf, plot(Rp)
grid on, title('Rows of the \pi-periodic part of f')

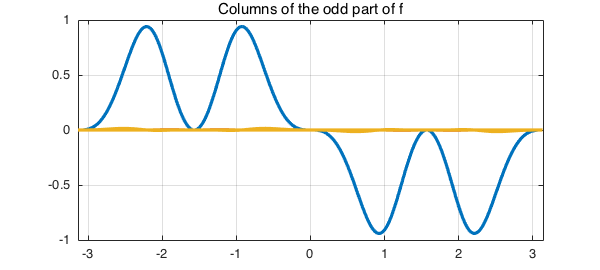
The other part of $f$, foa, has a CDR decomposition whose columns are odd and whose rows are $\pi$-anti-periodic:

[Co, D, Ra] = cdr(foa);
plot(Co),
grid on, title('Columns of the odd part of f')

clf, plot(Ra)
grid on, title('Rows of the \pi-anti-periodic part of f')

The integral of a spherefun is equal to the integral of its even/$\pi$-periodic piece, since the integral of any odd/$\pi$-anti-periodic spherefun is zero:

format long
sum_f = sum2(f)
sum_foa = sum2(foa)
sum_fep = sum2(fep)

sum_f =
   6.283185307179586
sum_foa =
     0
sum_fep =
   6.283185307179586

An equivalent partitioning is available for diskfuns [2].

References

1. A. Townsend, H. Wilber, and G. Wright, Computing with functions in spherical and polar geometries I. The sphere. SIAM J. Sci. Comput., 38 (2016) C403-C425.

2. A. Townsend, H. Wilber, and G. Wright, Computing with functions in spherical and polar geometries II. The disk, Submitted (2016).