[revised June 2019]

Chebfun is able to represent complex functions of a real variable, which lends itself very well to computing paths and path integrals in the complex plane. In this brief example we demonstrate this by integrating the function

f = @(x) log(x)*tanh(x);

around a 'keyhole' contour which avoids the branch cut on the negative real axis.

We'll first define our keyhole. Let $r$, $R$, and $e$ be the inner and outer radii and the width of the key respectively:

r = 0.2;   R = 2;   e = 0.1;

Construct the contour:

s = chebfun('s',[0 1]);                 % dummy variable
c = [-R+e*1i -r+e*1i -r-e*1i -R-e*1i];
z = join( c(1) + s*(c(2)-c(1)), ...     % top of the keyhole
          c(2)*c(3)^s/c(2)^s,   ...     % inner circle
          c(3) + s*(c(4)-c(3)), ...     % bottom of the keyhole
          c(4)*c(1)^s/c(4)^s);          % outer circle

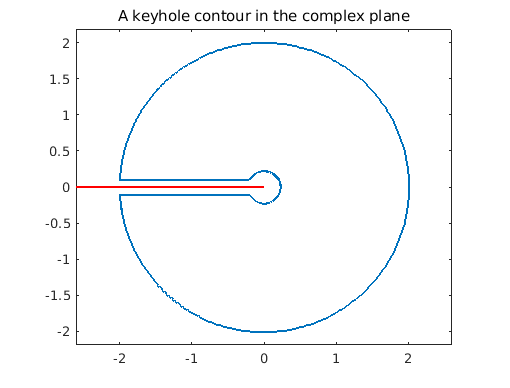
Plot the contour and the branch cut of the function $f$:

figure('position', [0 0 500 400])
plot(z), axis equal, title('A keyhole contour in the complex plane');
hold on, plot([-2.6 0],[0 0],'-r'); hold off, xlim([-2.6 2.6])

Now to integrate around the contour, we parametrise by a real variable, say $t$ (which here is done implicitly by the Chebfun representation), and integrate the function $f(z(t)) z'(t)$ with respect to $t$.

In Chebfun, this is easy:

I = sum(f(z)*diff(z))

I =
  0.000000000000007 + 5.674755637702212i

For the function we chose above, one can compute this integral exactly.

Iexact = 4i*pi*log(pi/2)

Iexact =
  0.000000000000000 + 5.674755637702224i

How does this compare with our computation?

error = abs(I - Iexact)

error =
     1.330964716833751e-14