A Mathematics Today column by Alan Champneys [2] describes a fascinating example that can be found in Wikipedia [4] and goes back to a paper by Rabinowitz [3]; see also [1]. Here is a bivariate polynomial $p(x,y)$:

tic
r2 = @(x,y) x.^2 + y.^2; xy = @(x,y) x.^2 - 3*y.^2;
p = @(x,y) r2(x,y).^4 - 45*r2(x,y).^3 - 41283*r2(x,y).^2 + ...
    7950960*r2(x,y) + 16*xy(x,y).^3 + 48*r2(x,y).*xy(x,y).^2 + ...
    x.*xy(x,y).*(16*r2(x,y).^2 - 5544*r2(x,y) + 266382) - 373248000;

The result is that the zero set of $p$ has constant width in the complex plane! -- like the British 50p coin. Let's verify this in Chebfun. Here's the domain, computed with the Chebfun2 roots command:

pc = chebfun2(p,[-11 11 -11 11]);
r = roots(pc);
copper = [.722 .451 .20];
fill(real(r),imag(r),copper)
axis(12*[-1 1 -1 1]), axis square, grid on

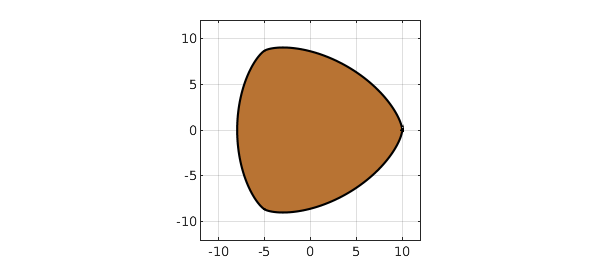
We compute its width measured in 5 different directions, and they agree to 5 digits, which is not bad considering the size of the coefficients.

disp('theta/pi     width')
for theta = pi*(0:4)/5;
   a = exp(1i*theta);
   width = max(real(a*r)) - min(real(a*r));
   fprintf('%8.5f %12.8f\n',theta/pi,width)
end

theta/pi     width
 0.00000  18.00727883
 0.20000  18.00041631
 0.40000  18.00052076
 0.60000  18.00086199
 0.80000  18.00028527

The exact result should be 18, as can be verified by setting $y=0$, in which case the polynomial reduces to

p = @(x) x^8 + 16*x^7 + 19*x^6 - 5544*x^5 - 41283*x^4 + 266382*x^3 + 7950960*x^2 - 373248000;

We confirm that this is zero at $x=-8$ and $x=10$:

p(-8)
p(10)

ans =
     0
ans =
     0

Just for fun let's compute the perimeter of the coin, presumably also accurate to about 5 digits:

perimeter = norm(diff(r),1)

perimeter =
  57.179193996908275

time_for_this_example = toc

time_for_this_example =
   3.371892000000000

[1] M. Bardet and T. Bayen, On the degree of the polynomial defining a planar algebraic curves of constant width, arXiv:1312.4358v1, 2013.

[2] A. Champneys, Westward Ho! Musing on mathematics and mechanics, Mathematics Today, April 2022, 56--59.

[3] S. Rabinowitz, A polynomial curve of constant width, Missouri Journal of Mathematical Sciences 9 (1997), 23--27.

[4] Wikipedia, "Curve of constant width".