A Vandermonde quasimatrix can be made like this in Chebfun:

x = chebfun('x');
A = x.^(0:10);

This particular example has 11 columns corresponding to the functions $1, x, \dots, x^n$ with $n=10$, and it is quite ill-conditioned:

cond(A)

ans =
     3.072959852624344e+03

In fact, the condition number grows exponentially as $n\to\infty$ at the rate $\rho_c^n$ with $\rho_c = 1+\sqrt 2$:

for n = 1:20
   c(n) = cond(x.^(0:n));
end
rhoc = 1+sqrt(2);
semilogy([c; rhoc.^(1:20)]','.-'), grid on
xlabel n, ylabel('condition number')
legend('Vandermonde matrix','asymptotics','location','northwest')

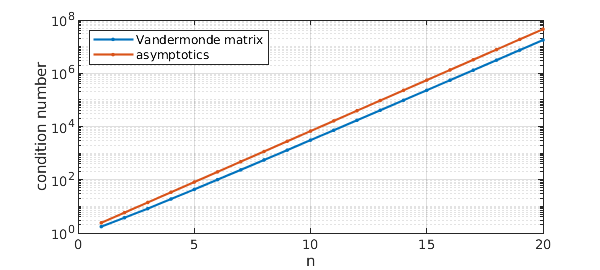
So far as I am aware, this growth constant $\rho_c$ was first identified by Walter Gautschi in 1975 [2, eq. (6.5)], and a much more complete theory has been provided by Beckermann [1, Thm. 4.1]. (These authors were working not with quasimatrices, but with discrete square matrices sampled at Chebyshev points. The crucial property of $\rho_c$ is that if the circle $|z|=\rho$ in the complex $z$-plane is mapped to an ellipse in the complex $x$-plane by the Joukowski map $x = (z+z^{-1})/2$, $\rho_c$ is the value of $\rho$ for which the ellipse just touches the unit circle. This happens at $x = \pm i$, the Joukowski images of $z = \pm i \rho_c$.

Here is an explanation of why this property controls the condition number. (It amounts to a proof that the condition number can grow no faster than this.) $A$ represents the map from coefficient vectors $c = (c_0,\dots, c_n)^T$ to polynomials $p(x) = c_0 + \cdots + c_n x^n$. The essential question for the condition number is, how small can $p$ be relative to $c$? Specifically, working in the $\infty$-norm for simplicity, if $|p(x)| \le \varepsilon$ for all $x\in [-1,1]$ but $|c_k|\ge 1$, for some $0\le k \le n$, how small can $\varepsilon$ be?

The answer comes from combining Cauchy's estimate with Bernstein's inequality of 1912, which can be found on p. 60 of Approximation Theory and Approximation Practice. Bernstein tells us that if $|p(x)|\le \varepsilon$ on $[-1,1]$, then $|p(x)| \le \rho^n\varepsilon$ on the $\rho$-ellipse for any $\rho>1$. In particular, we have $|p(x)| \le \rho_c^n\varepsilon$ on the $\rho_c$-ellipse. But since the $\rho_c$-ellipse contains the unit circle, we also have $|p(x)| \le \rho_c^n\varepsilon$ on the unit circle. On the other hand by Cauchy's estimate, for each $0\le k \le n$, we must have $|p(x)|\ge |c_k|$ for some $x$ on the unit circle. And thus we conclude $$ \varepsilon \ge \rho^{-n}. $$

[1] B. Beckermann, The condition number of real Vandermonde, Krylov and positive definite Hankel matrices, Numerische Mathematik 85 (2000), 553-577.

[2] W. Gautschi, Norm estimates for inverses of Vandermonde matrices, Numerische Mathematik 23 (1975), pp. 337--347.