function Crouzeix
Crouzeix's conjecture is a fascinating open problem in matrix theory, which bounds the size of a function of a matrix, $p(A)$. See [1].
Let $p$ be an analytic function, and in fact, it is enough to suppose $p$ is a polynomial. Let $A$ be a square matrix, and let $|\cdot|$ be the 2-norm on matrices. Crouzeix's conjecture is the inequality $$ |p(A)| \le 2|p|_{W(A)} $$ where $ |p(A)|_{W(A)} $ denotes the maximum of $|p(z)|$ where $z$ ranges over the field of values (or numerical range) of $A$. $W(A)$ is defined as the set of Rayleigh quotients associated with $A$, and there is a Chebfun command fov to compute it. This is a nonempty, bounded, convex set in the complex plane that contains the eigenvalues of $A$. For more about $W(A)$, see the Chebfun Example linalg/FieldOfValues.
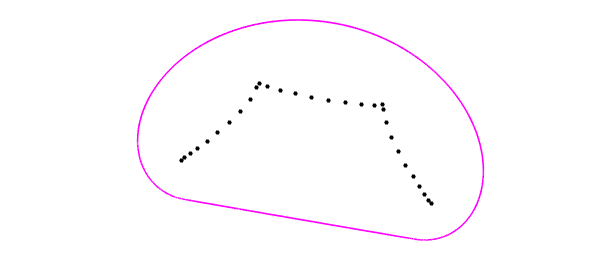
For example, here are the eigenvalues and field of values of the "Grcar matrix" of dimension $30$, rotated (for no particular reason) by multiplication by $\exp(1.4i)$.
A = exp(1.4i)*gallery('grcar',30);
plot(eig(A),'.k','markersize',16)
hold on, plot(fov(A),'m','linewidth',1.6)
hold off, axis equal, axis off
Intriguingly, the inequality of Crouzeix's conjecture has been established with a weaker constant [2]: $$ |p(A)| \le 11.08 |p|_{W(A)}. $$ Thus the challenge is to improve $11.08$ to $2$. This is the best possible constant, as we shall see in a moment.
It is known that Crouzeix's inequality holds in all kinds of special cases, including if $A$ has dimension $2$, if $A^2=0$, if $A^3=0$ and $d=3$ (Crouzeix 2012), if $W(A)$ is a disk (Badea 2004 based on work of von Neumann 1951 and Okubo and Ando 1975), if $p(z)=z^n$ (Berger 1965) and 1967, Pearcy 1966). or if $A$ is normal (in which case the constant $2$ can be improved to $1$ and the inequality is an equality). The case of matrices of dimension $3$ is open but has been explored so thoroughly numerically that if Crouzeix's conjecture is false, it is highly likely that the first counterexample is of dimension $4$ or higher.
Given a matrix $A$ and a polynomial $p$, let $c(A,p)$ be the "Crouzeix ratio" $|p(A)|/|p|_{W(A)}$. We can compute this in a single line of Chebfun!
c = @(A,a) norm(polyvalm(a, A)) / norm(polyvalc(a, fov(A)), inf);
Here $a$ is a vector of coefficients of $p$, ordered from highest to lowest degree in Matlab's usual fashion, and polyvalc is a function that evaluates a polynomial of a chebfun. (We should probably replace this with an overload of polyval for chebfuns.)
function pf = polyvalc(a,f) % evaluate polynomial of chebfun f
pf = a(end)*f.^0;
for k = 1:length(a)-1
pf = pf + a(end-k)*f.^k;
end
end
For example, here is an example that shows that the constant $2$ is best possible, namely $p(A) = A$ where $A$ is a Jordan block of dimension 2:
A = [0 1 ; 0 0]; a = [1 0]; c(A,a)
ans = 2.000000000000000
Here is a random matrix of dimension 20 with a random polynomial of degree 4:
rng('default'), A = randn(20)/sqrt(20);
a = randn(5, 1);
c(A,a)
ans = 1.191767399740756
Here is the same polynomial with the matrix B defined as a diagonal matrix, hence normal, with the same eigenvalues as A. In this case the Crouzeix ratio must be $1$.
B = diag(eig(A)); c(B,a)
ans = 1.000000000000000
We have done experiments with an optimization code to try to find counterexamples to Crouzeix conjecture for matrices of various dimensions, and so far, we have found no counterexamples.
end
References
-
M. Crouzeix, Bounds for analytical functions of matrices, Integral Equations and Operator Theory, 48 (2004), 461-477.
-
M. Crouzeix, Numerical range and functional calculus in Hilbert space, Journal of Functional Analysis, 244 (2007), 668-690.

