Sometimes one needs to find the roots of a rational function expressed in partial fraction form, like this:

$$ r(x) = 1 + \sum_{j=0}^N \frac{a_j}{b_j-x} . $$

For example, a "secular equation" of this kind arises in numerical linear algebra as part of the divide and conquer algorithm for computing eigenvalues of symmetric matrices (see [1] and p. 231 of [2]). If the coefficients $a_j$ are positive and the poles $b_j$ are distinct, then $r$ must switch from $+\infty$ to $-\infty$ as $x$ passes through each pole, and it follows that $r$ has exactly $N-1$ real zeros lying between the poles and also one more real zero lying to the right of all the poles.

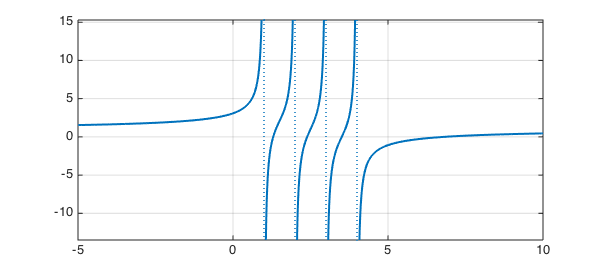
Here is an example with $N=4$:

x = chebfun('x',[-5 10]);
for j = 1:4
  f = 1 + 1./(1-x) + 1./(2-x) + 1./(3-x) + 1./(4-x);
end
hold off, plot(f,'linewidth',2), grid on

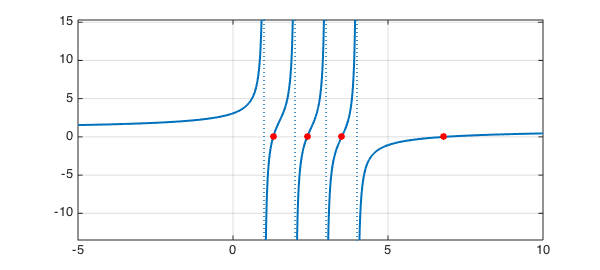
Chebfun can compute the roots:

format long, format compact
r = roots(f)

r =
   1.000000000000000
   1.296089645312119
   2.000000000000000
   2.392275290272984
   3.000000000000000
   3.507748705363648
   4.000000000000000
   6.803886359051248

Notice that the result is 8 numbers, including the poles as well as the roots. This is because Chebfun's convention is to regard a function as having a root at any point where it crosses between positive and negative values. If we don't want roots of that kind, we can execute instead

r = roots(f,'nojump')

r =
   1.296089645312119
   2.392275290272984
   3.507748705363648
   6.803886359051248

Let us add the roots to the plot.

hold on, plot(r,f(r),'.r','markersize',24)

References

1. J. J. M. Cuppen, A divide and conquer method for the symmetric tridiagonal eigenproblem, Numerische Mathematik 36 (1980/81), 177-195.

2. L. N. Trefethen and D. Bau, III, Numerical Linear Algebra, SIAM, 1997.