The function $$ f(x) = \int_0^{\infty} {e^{-t} \over 1 + xt} dt $$ is an easy one for Chebfun to evaluate. For example, the value at $x=1$ is
format long sum(chebfun(@(t) exp(-t)/(1+t),[0 inf]))
ans = 0.596347362323193
It's not hard to make a Chebfun of the result, like this:
ff = @(x) sum(chebfun(@(t) exp(-t)/(1+x*t),[0 inf]));
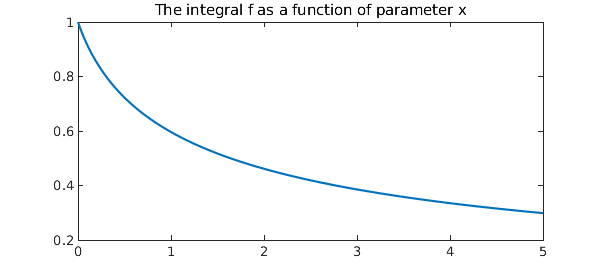
f = chebfun(ff,[0,5]);
hold off, plot(f)
title('The integral f as a function of parameter x')
One of the interesting features of $f$ is that its derivatives at $x=0$ are $(0!)^2, -(1!)^2, (2!)^2, -(3!)^2, \dots.$ Chebfun manages to compute a few of these, at any rate, to good accuracy:
for j = 0:6
fj = diff(f,j);
fprintf('%21.12f (should be %7.0f)\n',fj(0),(-1)^j*factorial(j)^2)
end
1.000000000000 (should be 1)
-0.999999999998 (should be -1)
3.999999996404 (should be 4)
-35.999996324084 (should be -36)
575.997547930357 (should be 576)
-14398.796599478534 (should be -14400)
517929.744379208831 (should be 518400)
In other words, at $x=0$, $f$ has the asymptotic series $$ f(x) \sim 0! - 1!x + 2!x^2 - 3! x^3 + \cdots . $$ It can't be a Taylor series, because the terms increase too fast: the radius of convergence is zero.
And this brings us to the famous old problem of divergent series, going back to Euler in 1760 and with its own entry in Wikipedia [1]. What is the value of the series $$ 0! - 1! + 2!- 3! + \cdots = ~? $$ Of course the series simply doesn't converge, from one point of view. But this didn't stop Euler and Hardy and many others from discussing what it might mean for such a series to have a limit. And of course we know one pretty good candidate for an answer, namely the value $f(1)$ computed above:
f(1)
ans = 0.596347362323191
Suppose we try to estimate this limit from those not-quite-Taylor coefficients. We could use the epsilon algorithm, which amounts to constructing a Pade approximation and evaluating it at $z=1$. Here's the result, showing 2 digits of accuracy:
r = padeapprox((-1).^(0:10).*factorial(0:10),5,5); r(1)
ans = 0.597383362132805
At $z=1/2$ we get 3 or 4 digits:
f(0.5) r(0.5)
ans = 0.722657233776442 ans = 0.722739361702127

