LW = 'linewidth'; dom = [0 2*pi];
Chebfun uses Fourier collocation to solve linear, nonlinear and systems of ODEs with periodic boundary conditions. Consider the nonlinear ODE
$$ u' - u\cos(u) = \cos(4x), $$
on $[0, 2\pi]$, with periodic boundary conditions. For nonlinear ODEs, we need to specify an intial guess; let us try $\cos(x)$. We can solve the ODE in Chebfun as follows.
f = chebfun(@(x) cos(4*x), dom); N = chebop(@(u) diff(u) - u.*cos(u), dom); N.bc = 'periodic'; N.init = chebfun(@(x) cos(x), dom); u = N \ f
u =
chebfun column (1 smooth piece)
interval length endpoint values trig
[ 0, 6.3] 89 -0.058 -0.058
Epslevel = 2.331417e-15. Vscale = 2.428494e-01.
Let us plot the initial guess in dashed blue, and the solution in blue.
figure, plot(N.init, '--b', LW, 2) hold on, plot(u, 'b', LW, 2)
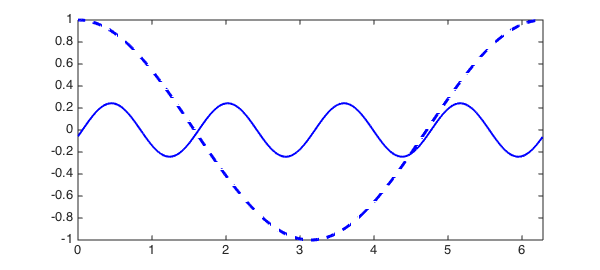
The solution $u(x)$ satisfies the ODE to high accuracy:
norm(N*u - f, inf)
ans =
3.379422527647751e-12
If we start with another initial guess, we might obtain another solution. Let us try $\sin(x)^2$, plot it in dashed green, and plot the solution in green.
N.init = chebfun(@(x) sin(x).^2, dom); v = N \ f hold on, plot(N.init, '--g', LW, 2) hold on, plot(v, 'g', LW, 2)
v =
chebfun column (1 smooth piece)
interval length endpoint values trig
[ 0, 6.3] 81 1.6 1.6
Epslevel = 1.776357e-15. Vscale = 1.785953e+00.
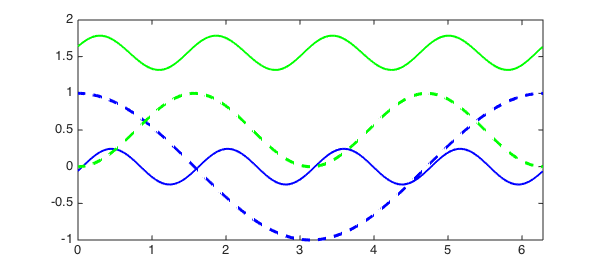
The solution $v(x)$ satisfies the ODE to high accuracy too:
norm(N*v - f, inf)
ans =
1.803868478825869e-12
For nonlinear ODEs, the relationships between intial guesses and solutions are difficult to analyse. In this example, we chose two different guesses, and this led to two different solutions.

